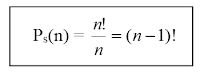Perbandingan Trigonometri pada Segitiga Siku-Siku

 Jika berbicara tentang dasar trigonometri, mutlak kita akan berhadapan dengan segitiga siku-siku, karena trigonometri itu sendiri didefinisikan berdasarkan konsep kesebangunan pada segitiga siku-siku.

Diberikan segitiga ABC siku-siku di B dengan ∠ A = θ.

Jika sisi di depan sudut (opposite) dinamakan "depan", sisi di samping sudut (adjacent) dinamakan "samping" dan sisi miring (hypotenuse) dinamakan "miring", maka perbandingan sisi-sisi tersebut didefinisikan sebagai berikut :

Keterangan :
sin untuk sinus
cos untuk cosinus
tan untuk tangen
csc untuk cosecan
sec untuk secan
cot untuk cotangen

Catatan :
Sisi depan dan sisi samping dapat berubah tergantung sudut yang digunakan, sedangkan sisi miring selalu sama, yaitu sisi terpanjang dan letaknya selalu di depan sudut siku-siku.

contoh:

Video pembelajaran

Kerjakan Quiznya Klik disini !

Semoga Bermanfaat Untuk Kemajuan Bersama ^_^

Kombinasi

 

Saksikan video pembelajaran berikut

Kerjakan Quiznya Klik disini !

Semoga Bermanfaat Untuk Kemajuan Bersama ^_^

Trigonometri ( Satuan sudut )

 A. Ukuran Sudut 

1. Ukuran Derajat Besar sudut dalam satu putaran adalah 360°. Berarti 1°= 1/360 putaran. Ukuran sudut yang lebih kecil dari derajat adalah menit ( ‘ ) dan detik ( “ ). 

Hubungan ukuran sudut menit, detik, dan derajat adalah:

2. Ukuran Radian Satu radian adalah besar sudut pusat busur lingkaran yang panjangnya sama dengan jari-jari.

3. Hubungan Derajat dengan Radian Untuk mengubah sudut ke dalam satuan radian, menggunakan rumus:

Dan untuk mengubah sudut sebesar X radian ke dalam satuan derajat, menggunakan rumus:

Kerjakan Quiznya Klik disini !

Semoga Bermanfaat Untuk Kemajuan Bersama ^_^

Permutasi

Permutasi adalah susunan objek-objek dengan memperlihatkan urutan tertentu.

a. Permutasi n objek berbeda yang setiap kali diambil seluruhnya (_nP_n)

Contoh:

Diketahui 3 abjad pertama yaitu A, B dan C. Berapa banyak susunan yang mungkin dari 3 huruf yang berbeda itu ?

 

Jawab:

₃P₃ = 3! = 3.2.1 = 6 cara

 

Contoh:

Diketahui 4 siswa : Ary, Ani, Ali dan Asih akan ditempatkan pada 4 buah kursi. Ada berapa cara untuk menempatkan siswa itu pada kursi yang berbeda ?

Jawab:

Kursi I dapat diisi oleh salah satu siswa dalam 4 cara.

Kursi II dapat diisi oleh salah satu siswa dalam 3 cara.

Kursi III dapat diisi oleh salah satu siswa dalam 2 cara.

Kursi IV dapat diisi oleh salah satu siswa dalam 1 cara.

Sehingga dengan prinsip dasar probabilitas, keempat kursi dapat ditempati oleh keempat siswa dengan :  4 x 3 x 2 x 1 = 24 cara.

Atau:

nPn = 4P4 = 4! = 4.3.2.1 = 24 cara.

 

b. Permutasi n objek berbeda yang setiap kali diambil sebagian (nPr)

Banyak permutasi n objek yang diambil r objek (0 < r < n) dinotasikan nPr atau P(n, r)  atau nPr (dibaca Permutasi r dari n) adalah :

Contoh:

Berapa banyak permutasi yang terdiri atas 2 huruf yang berbeda dari 4 huruf : A, I, U, E.

Jawab:

c. Permutasi n objek yang tidak semua berbeda

            Banyaknya cara menyusun unsur dalam suatu baris, jika ada p unsur yang sama dari satu jenis, q unsur dari jenis lain, dan seterusnya adalah :

Contoh:

Berapa carakah 5 huruf dari kata CUACA dapat disusun dalam suatu baris !

Jawab:

Unsur-unsur yang sama : huruf C ada 2, huruf A ada 2.

d. Permutasi Siklis

Banyaknya cara menyusun n objek berlainan dalam suatu lingkaran, dengan memandang susunan yang searah putaran jarum jam dan berlawanan arah putaran jarum jam adalah :

Contoh:

Terdapat berapa carakah empat anak A, B, C, D yang duduk melingkar dapat disusun dalam lingkaran ?

Jawab:

Cara I

Ambil seorang anak untuk diletakkan pada posisi yang tetap, kemudian menyusun tiga anak yang lain dalam tempat yang berbeda, maka cara ini dapat dilakukan dalam 3! = 3.2.1 = 6 cara.

Cara II

Perhatikan gambar !

Jika keempat anak itu diletakkan pada posisi 1, 2, 3 dan 4 bergantian searah putaran jarum jam dalam sebuah lingkaran , maka mereka tetap membentuk susunan yang sama. Karena itu, penyusunannya harus menempatkan seorang anak kepada posisi yang tetap dan menggerak-gerakkan posisi tiga anak yang lain.

Semoga Bermanfaat Untuk Kemajuan Bersama ^_^

Kerjakan Quiznya Klik disini !

Kaidah Pencacahan

 1. Prinsip Dasar Membilang

    Jika suatu operasi terdiri dari 2 tahap, tahap pertama dapat dilakukan dengan m cara yang berbeda dan tahap kedua dapat dilakukan dengan n cara yang berbeda, maka keseluruhan operasi dapat dilakukan dengan m x n cara. Cara pencacahan seperti ini disebut kaidah perkalian.

 Contoh:

Berikut ini jalan yang dapat dilalui pengendara motor dari kota A ke kota C melelui kota B.

Ada berepa cara yang dapat dilakukan dari A ke C ?

Jawab:

Dari A ke B dapat dilakukan dengan 4 cara.

Dari B ke C dapat dilakukan dengan 3 cara.

Jadi, dari A ke C dapat dilakukan dengan = 4 x 3 = 12 cara, yaitu:

    jalan 1,5 ; jalan 1,6 ; jalan 1,7

    jalan 2,5 ; jalan 2,6 ; jalan 2,7

    jalan 3,5 ; jalan 3,6 ; jalan 3,7

    jalan 4,5 ; jalan 4,6 ; jalan 4,7

2. Faktorial

      Hasil kali bilangan bulat positif (bilangan asli) berturut-turut dari n sampai 1 disebut n faktorial, ditulis : n!

       

      

Kerjakan Quiznya Klik disini

Semoga Bermanfaat Untuk Kemajuan Bersama ^_^

TRIGONOMETRI (Sesi 1)

 Perbandingan trigonometri

A. Nilai Perbandingan Trigonometri

Perhatikan segitiga berikut !

  

Selanjutnya nilai perbandingan trigonometri suatu sudut segitiga dapat ditentukan dengan menggunakan daftar / tabel dan kalkulator.

B. Nilai Perbandingan Trigonometri Untuk Sudut-sudut Istimewa

Perhatikan gambar berikut !

    

    

Kerjakan Quiznya Klik disini

Semoga Bermanfaat Untuk Kemajuan Bersama ^_^